The first time computers beat mathematicians to a proof
The hundred-year story of the four-colour theorem
Here’s a fun fact that feels like it shouldn’t be true:
No matter how complicated a map is, you never need more than four colours to colour it so that no two neighbouring regions share the same colour.
This is the essence of the Four Colour Theorem, one of the most famous results in topology and graph theory. At first glance it sounds like a cute puzzle. In reality, it turned out to be one of the hardest problems of the 20th century — and no one succeeded in solving it until computer-assisted proofs entered the game.
What this problem says … And doesn’t say
What it says
Take any map; delimitations (boundaries) on this map define regions. Each region is adjacent to number of other regions, meaning that they share a common boundary that is not a point; two regions that share isolated boundary points are not considered as adjacent.
Then the Four Colour Theorem states:
Any map can be coloured with at most four colours, so that no two adjacent regions share the same colour.
For the more mathematically-minded around you:
Here boundaries on the map are assumed to be finite unions of differentiable curves (‘real-life’ boundaries in the real plane); we forbid ‘regions’ delimitated by esoteric boundaries such as topological curves with infinite length. In particular, if you associate to each region of the map a vertex, and connect two vertices if the associated regions are adjacent, the Four Colour Theorem states that you can colour the vertices of the associated graph with only four colour, so that no two adjacent vertices receive the same colour.
What the problem doesn’t say.
It doesn’t state that you can colour country maps with 4 colours. Indeed, the cartography convention for colouring countries is that you always colour two regions belonging to the same country in the same colour even if the region is not adjacent to the ‘main’ part of the country.
And the four colour theorem isn’t true in that setting! You’ll usually need more than 4 colours to colour a ‘country map’. For example France and Netherlands share a boundary (in the Saint Martin island), which implies that countries in Europe need to be coloured with at least five different colours.
Some examples
Let us go to some examples together.
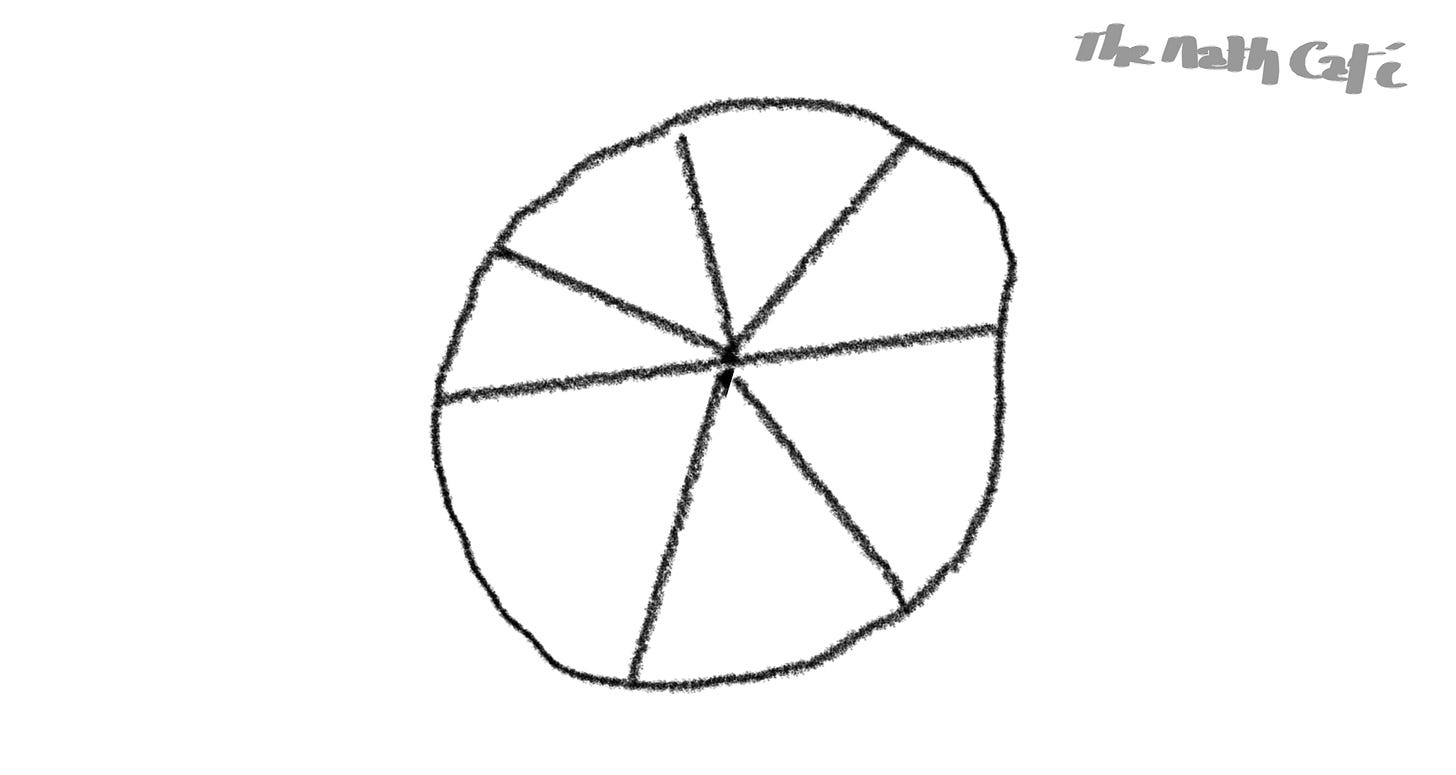
First, let us consider this pie:
Notice you can colour it using only three colours! (Remember that regions that share only points aren’t considered adjacent, so only consecutive ‘slices of the pie’ are considered adjacent)
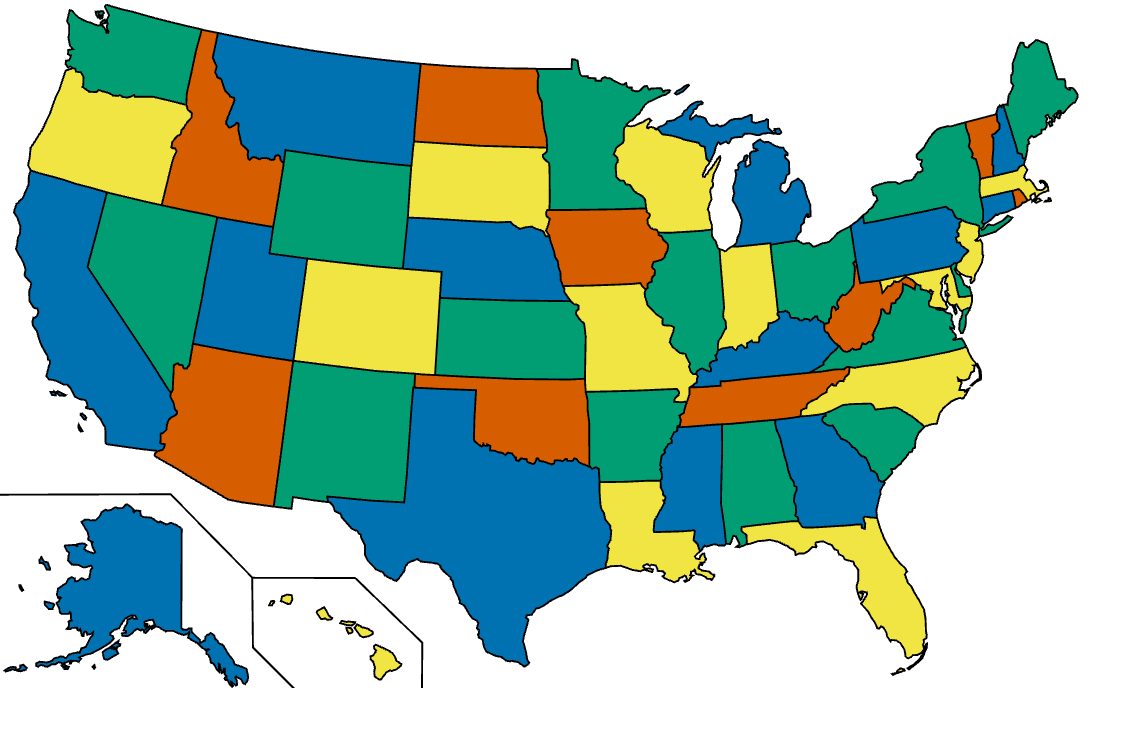
Now let us consider the map of the USA. One possible colouring with four colours is:
So we can colour the USA map using only four colours.
Let us think a bit more…
Can we use less than four colours?
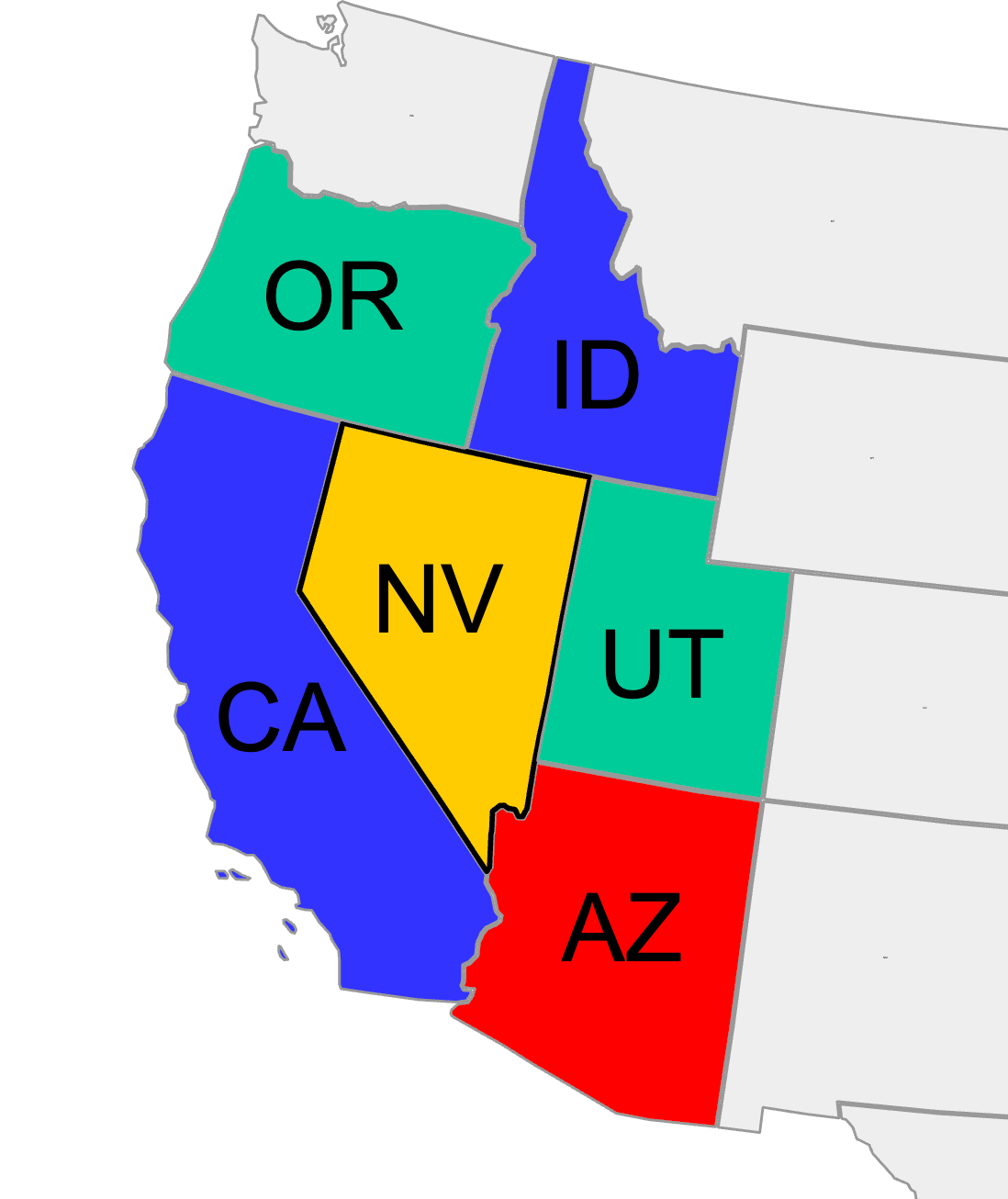
The answer is no. You can prove it by considering the regions surrounding the Nevada state:
Let us pick a colour for the Nevada state (yellow in the map under).
Then necessarily all five neighbouring states are coloured in colours other than yellow.
We need three different colours at least to colour them (if you go through all the possibilities for two colours you always end up colouring two adjacent states with the same colour — which is a colouring style we have forbidden).
Your turn!
Difficulty: ☕☕
The sketch/map under has been coloured using five colours. Can you colour it using four colours only?
(Scroll down for the solution…)
A hundred-year history
A problem from the age of hand-drawn maps
Back in 1852, a British student named Francis Guthrie noticed while colouring a map of counties that four colours always seemed to be enough. He asked his brother, who asked mathematician Augustus De Morgan, who asked the wider mathematical community… and nobody could prove it.
For over a century, mathematicians tried—and failed—to show that there exists no map requiring five colours.
The surprising twist
After decades of partial progress, the breakthrough came in 1976 from Kenneth Appel and Wolfgang Haken.
They used a mix of old ideas along with the the new computing power of computers: instead of proving the theorem “by hand,” they reduced the problem to a finite but enormous set of special cases and checked them using a computer. If no counterexample exists among those cases, then no counterexample exists at all.
It was the first major theorem proven with essential computer assistance—causing both excitement and controversy. Some mathematicians were uncomfortable: could a proof be trusted if no human could check every line?
Today, the Four Colour Theorem is widely accepted, and later work has simplified and reverified the computational parts. But the debate about what counts as a “proof” still echoes in modern discussions about machine-verified mathematics.
What about human proofs?
Several mathematicians have tried providing a 100% human-written proof — with little success so far. Thomassen provided a beautiful proof in the 90s that every map can be colour with five colours only, but the four colour case remains in the realm of computers. This reminds us of how crucial computer assistance can be even in the most theoretical areas of science.
What makes this theorem beautiful
Beyond the historical drama, the theorem touches on deep ideas.
Maps are really just graphs in disguise. Regions become nodes; shared borders become edges. The theorem says that planar graphs (graphs that can be drawn without edges crossing) are four-colourable. It pushed forward the development of graph colouring, a very active field of research in graph theory.
It has applications in many practical areas (you probably use it every day), including:
Scheduling and timetabling tools (softwares ensuring there are no conflicts in time slots/ room booking);
Registering allocation in compilers (used for example by your web browser compiler, every day billions of people use these tools without knowing about it);
Cloud resource allocation;
Computer graphics/mesh colouring.
In the meantime, the proof forced mathematicians to invent new combinatorial tools and pushed the development of computational proof verification.
And yet—despite all the complexity—its statement remains disarmingly simple.
You can explain it to a child with a pack of coloured pencils (… and a lot of patience).
The Four Colour Theorem is a reminder that even problems that look naïve or recreational can open the door to deep mathematics. Some of the most profound discoveries start with curiosity, a simple question, or even… a map someone was trying to colour neatly.
📅 Next week
Next Tuesday, we will discuss a nice paradox involving your birthday date.
Until then, I wish you a beautiful, blessed week 🌸.
With love and curiosity,
Sybille